Теория линий второго порядка и использования ИКТ в обучении

где . Из (20) следует, что

Рассмотрим два случая:

Пусть , тогда , то есть (21)

где

Положим , тогда уравнение (21) примет вид:

Это каноническое уравнение параболы, симметричной относительно

оси (OY ).

Пусть , тогда уравнение (20) перепишется в виде

(22)

1. Если , то получим уравнение оси (OY ) .

2. Если , то возможны два случая. Если A′ и F′ одного знака, то точек, удовлетворяющих данному уравнению, нет; если же A′ и F′ разных знаков, то , где , поэтому и уравнение (22) описывает две параллельные прямые: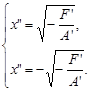

b) Пусть , тогда уравнение (9) примет вид

(23)

Если , а , то точек, удовлетворяющих уравнению (23), нет; если же или отличны от нуля, то уравнение (23) описывает прямую.

Вывод. Путем преобразований кривой второго порядка, определяемой уравнением (1) мы можем получить уравнения таких линии второго порядка, как:

- уравнение эллипса

- уравнение гиперболы

- уравнение параболы

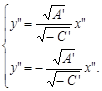- совокупности двуз пересекающихся прямых

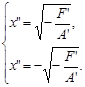- совокупности двух параллельных прямых

Содержание темы «Линии второго порядка» в элементарной математике

В математике рассматриваются линии второго порядка, как конические сечения: окружность, эллипс, гипербола, парабола; или как множество точек обладающих некоторыми свойствами.

Рассмотрим каждую линию второго порядка подробнее, определяя линии как множество точек.

Окружность

Определение 1.1. Окружность - множество точек плоскости, равноудаленных от данной точки М0, называемой ее центром.[9.С.65]

Общий вид уравнения

Исследование свойств окружности по её уравнению

Пресечение с осями координат:

С ОХ: Пусть у=0, тогда . Отсюда делаем вывод, что (-R;0), (R;0)- точки пересечения с осью ОХ.

С ОУ: Пусть х=0, тогда 02+у2=R2. Отсюда делаем вывод, что (0;-R),(0;R)- точки пресечения с осью ОУ.

Следовательно, у окружности с центром в начале координат область допустимых значений для и для закрытый интервал .

Вывод: Окружность вписана в квадрат с размером стороны 2R.[1.С.99]

2) Симметрия окружности:

Относительно оси ОХ и оси ОУ, так как окружность имеет общие точки пересечения с осями координат.

Пусть принадлежит окружности, т. Е - верное равенство.

Точка симметрична точке М0 относительно оси ОХ. Подставим координаты точки М1 в уравнение окружности ,отсюда имеем: - верное равенство.

Следовательно, М1 принадлежит окружности, отсюда следует, что окружность симметрична относительно оси ОХ.

Еще о педагогике:

Диагностика протекания адаптационного процесса детей шести лет к обучению в школе
Объектом исследования являлись ученики в количестве 20 человек МОУ СОШ №1 с. Канглы Минераловодского района посещавшие подготовительные к школе курсы и зачисленные этим же составом в 1А класс. Результаты обследования представляются в виде количественных оценок, которые получает ребенок за каждое за ...

Школьный балл - проблемы и решения
Исторический анализ показал, что зачастую под отметкой в российском образовании понималась оценка и наоборот. Однако шкала отметок более жестка, формализована. Ее главная задача установить уровень (степень) усвоения школьником единообразной государственной программы, образовательного стандарта. Она ...

Методики изучения развития речи детей с нарушением интеллекта
Реализация прав ребенка, согласно конвенции ООН, которой следует и Россия, в первую очередь направлена на обеспечение всех детей, в том числе детей с выраженными отклонениями в развитии и инвалидов, полноценной общественной жизнью, на создание условий, необходимых для их максимальной реализации сво ...